Many assumptions in supply chain planning are expressed as hard-and-fast numbers although, in reality, there is a range of possible outcomes. A demand forecast of 100 pieces does not mean that we will sell exactly 100 pieces. It means that sales are estimated to be around 100 pieces, more or less. Sometimes a lot more, sometimes a lot less.
Demand is the main source of uncertainty in supply chains, but it is not the only one: shipments can be late; suppliers may not be able to deliver in full; pallets fall off forklifts and break. A supply chain executive once described his work as: “It’s disasters every day, and I love it”.
It is a lot easier to love daily disasters, though, when you are well prepared.
In this white paper, we will explain how and when to tackle uncertainty in supply chains by applying stochastic planning (and when you shouldn’t). We will focus on demand uncertainty as this is a problem shared by all companies, but you can apply the same approaches to manage other sources of uncertainty as well.
What is Stochastic Planning?
The word stochastic refers to something that cannot be exactly predicted because it contains a component of randomness. Stochastic planning means preparing for a range of potential outcomes in an effective way.
In their latest Hype Cycle for Supply Chain Planning Technologies, Gartner positions stochastic supply chain planning as “sliding into the trough of disillusionment”. This means Gartner analysts expect it will take five to ten years for stochastic supply chain planning to contribute significantly to productivity.
However, as most concepts in supply chain management, stochastic planning is not a novel idea. It can be seen as a continuum ranging from well-established practices to more recent innovations fueled by advances in technology. Next, we will look at some concrete examples.
Stochastic Planning for Optimal Inventory
If we were to treat our demand forecast as a fact – i.e. if a sales forecast of 100 pieces would mean that we would stock exactly 100 pieces to meet this expected demand – we would not fare very well in meeting customer expectations. Even if our demand forecast was very accurate and the forecasted quantity was, on average, right, we would still fail to meet customer demand on a regular basis due to random variation in demand.
This is no news to inventory management professionals. Both the problem and its remedy – safety stock – are well-known and part of the standard supply chain curriculum. (The same thinking applies to lead time variation with the solution being safety lead time.)
An effective safety stock level protects us from most stock-outs without causing excessive inventory cost. Statistical analysis is the most common way of optimizing safety stock levels. By analyzing the mean value and distribution of sales or forecast errors, the amount of buffer stock needed to meet an availability target of, say 98%, can be calculated. Modern supply chain planning software automatically factors in the impact of batch sizes, review intervals and lead times in the calculation for more accurate results.
Advances in the analytics capabilities of supply chain planning software have, however, made it possible to set safety stocks even more accurately:
1. Not just one probability distribution: Traditionally, statistical safety stock calculations have relied on the assumption that demand is normally distributed. Especially for best-selling products, the normal (also known as Gaussian) probability distribution captures demand patterns quite accurately. However, in some situations, especially for low-selling items, other distributions, such as the negative binomial distribution, may offer a better fit. New analytics capabilities have made it feasible to identify and apply other probability distributions or even completely customized demand models when optimizing safety stocks.
2. Dynamic safety stocks: For example, in retail, sales often vary according to the weekday. If sales of a perishable product, say artisan bread, are around 8 pieces on a Monday and around 35 pieces on a Saturday, the safety stock level for Monday needs to be smaller than the safety stock level for Saturday. Increasing computational power has made it possible to manage not only forecasts, but also safety stock levels on the store-item-day level, allowing safety stock levels to move in step with demand.
3. Probabilistic order optimization: Safety stock calculations use an availability target as input. Often, it is feasible to identify the right availability level for different kinds of products based on, for example, a sales value (ABC) or a sales frequency (XYZ) classification. Sometimes, however, it can be quite complicated to find the right availability targets.
A good example of this is replenishment planning of perishable products in food retail. Even products within the same product group, say yogurt, can have very different shelf lives and, thus, different risk of spoilage. In addition, varying store sizes and locally optimized assortments mean that different stores may have more or less substitute products on offer. This has a direct impact on the risk of stock-outs causing lost sales.
With increased analytics capabilities and computing power, it has become feasible to optimize each replenishment order to minimize the total cost of stock-outs and excess stock based on the probability of the different outcomes. In food retail, this means balancing the risk of spoilage costs against the risk of lost sales margin. The cost function needs to be adjustable in terms of how much weight it places on on-shelf availability vs. waste to allow for considering the strategic roles of key categories and items as well as whether there are many or limited opportunities for substitution within the product category.
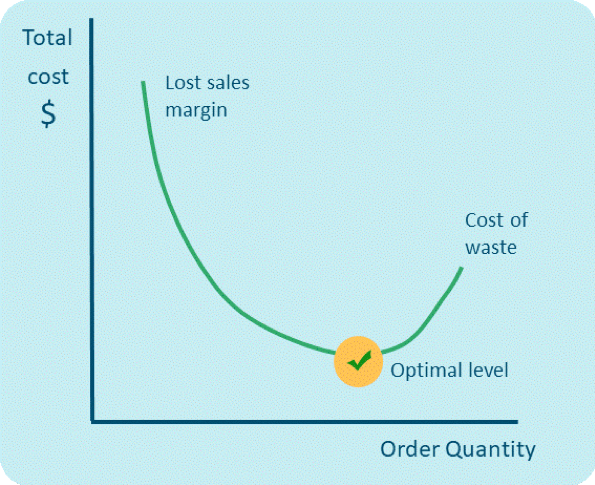
Does all this math sound complicated? The good news is that everything you know about using safety stock (or time or capacity buffers) to protect you from random variation still holds true. New technology just makes it easier for you to find more optimal safety stock levels!
Stochastic Planning in Multi Echelon Supply Chains
So far, we have presented approaches to dealing with demand uncertainty when optimizing inventory in one warehouse or a store. How is managing supply chains with multiple echelons, such as distribution centers that supply stores, different?
A Stochastic Problem or Simply a Disconnected Supply Chain?
Let’s start by disclosing an uncomfortable secret: A lot of the uncertainty in supply chains is self-inflicted!
Retail distribution is a good example of this: All too often, store replenishment and inventory management at the distribution centers or central warehouses are managed as separate processes, driven by separate demand forecasts. Demand planners at the distribution centers spend a lot of time trying to guess how stores will stock-up for the upcoming promotion, when the stores will start displaying seasonal products, and how long the first case packs of a new product will last until the stores will need replenishing.
Guessing what the stores will do is not a stochastic problem. It is a problem of poor supply chain management.
Best practice is to base distribution center forecasting on the stores’ projected orders, which reflect both pull-based demand as well as planned, push-based stock movements. According to a recent survey, only 14 % of the responding North American grocery retailers have implemented this best practice.
To achieve seamless integration of store and distribution planning, the supply chain planning system needs to be able to calculate projected store orders per product, store and day several months or even a year into the future. Moreover, the calculations need to reflect current and known future replenishment parameters (such as safety stocks, batch sizes, and replenishment schedules), forecasted demand, as well as planned inventory movements (such as stocking up stores prior to product launches, promotions or seasons). These calculations are quite feasible, but require significant data processing capacity, which is likely to be one explanation for the surprisingly low adoption rates.
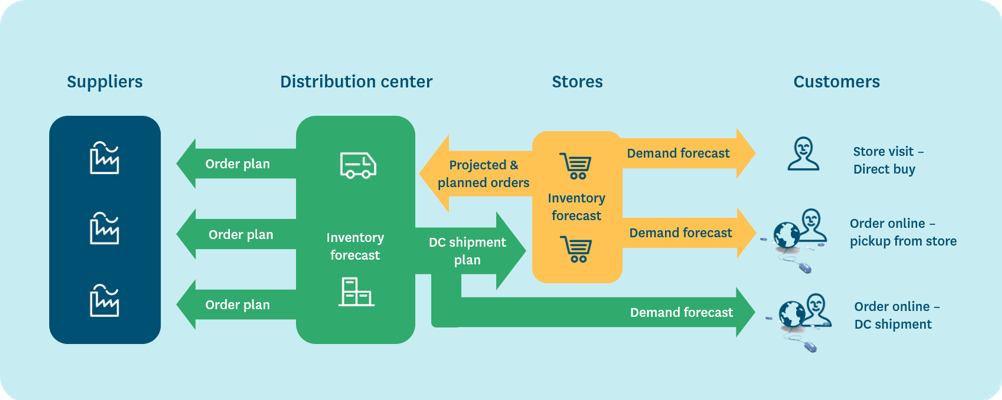
The same approach is, of course, applicable to securing availability from upstream suppliers by giving them access not only to estimated annual purchase quantities, but to the latest purchase order projections.
Stochastic Planning for Slow Movers
When projected orders are aggregated across stores, they form a very accurate, customer-driven forecast for the distribution centers supplying the stores. However, for very slow-moving products, this approach may introduce systematic bias to the upstream forecast.
This bias is a problem that can be solved with stochastic planning.
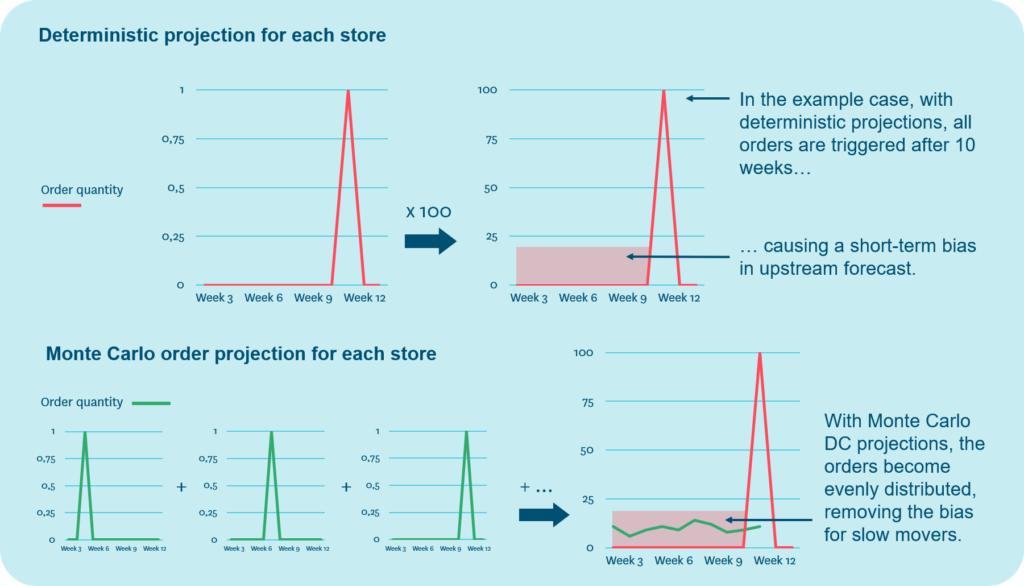
Let’s take an example: A slow mover sells on average 0.1 units per week. When the store sells one more unit of the product, the product’s inventory balance will drop low enough to trigger a replenishment order. Based on the forecast, the order is projected to happen 10 weeks from now. However, as demand for this slow mover is essentially random, the stores are equally likely to sell that order-triggering unit next week, or three weeks from now, or ten weeks from now. This means that the order projections, especially when aggregated across several stores with similar demand patterns, systematically underestimate near-term demand for slow movers.
A modeling approach called Monte Carlo sampling can be applied to distribute the projected replenishment orders of slow-moving products evenly over time. From the individual store’s perspective, this makes no difference; the store still needs to carry the same amount of safety stock to ensure availability. However, at the distribution center level, the forecast accuracy of slow movers is significantly improved.
When is Stochastic Planning Not Applicable?
Up to now, we have discussed the everyday uncertainty essentially caused by random variation in demand or processes. How about the really big disasters, like major hurricanes, strikes, or production plants going up in flames?
Well, the short answer is that stochastic planning is not applicable to these kinds of one-off disasters.
Stochastic planning is based on probability distributions. And to make use of probability distributions there needs to be a lot of data, such as historical sales, delivery or manufacturing data, available for modeling the probability of different outcomes. Such a track record of past events is, thankfully, not available for the really big disasters.
However, there are other approaches, such as scenario planning based on digital twin technology that allows you to compare different scenarios, such as a hurricane hitting a town at different levels of severity, and make judgment calls on how to prepare for potential disasters or find the best action in a critical situation.
Fancy Math is Cool, but Understanding the Problem is More Important
Modeling is obviously fun and more advanced math means cooler solutions, right?
Before getting excited about probability distributions and rushing away to dust off your old statistics textbooks, it may be good to reiterate a few points from the previous sections:
1. Not all supply chain uncertainty problems are good candidates for stochastic planning.
- Sometimes you need to fix the supply chain planning process rather than try to apply fancy modeling to uncertainty produced by a disconnected supply chain.
- Stochastic planning is applicable to processes for which you have historical data, such as consumer demand or manufacturing processes. Factory fires should not fall into this category.
2. Stochastic planning sounds fancy, but it is basically the same good old idea of using buffers of stock, time or capacity (whichever makes most sense in a given scenario) to mitigate the impact of random variation.
- The more advanced math simply makes the buffering more effective.
Sources:
Negative Binomial Distribution
Hype Cycle for Supply Chain Planning Technologies by Gartner, 2017
Are You Wasting Time and Money on a Poorly Integrated Supply Chain?
Winning the Food Fight: Best Practices for Managing Grocery Retail Supply Chains





